テンソルって何？

テンソルのイメージ

テンソルを勉強するときに一番最初に「・・・で、テンソルって結局何なの？」といった疑問が出てくるかもしれません。また、2階のテンソル、4階のテンソルといった概念も勉強していくと出てくるので、より「訳が分からない・・・」という悪循環になることもあるかもしれません。

テンソルは「ベクトルを拡張したもの」と説明されることが多いように思います。もちろん、これも正しい説明かと思います。

あるいは「存在そのもの」といった説明があるかもしれません。私はこっちの方が好きです。

構造力学では，「応力」はテンソルです。構造力学の学部くらいで習うだろう「モールの応力円」で明らかなように、物体に応力が働いているとき、ある切断面では，垂直応力やせん断応力が働いています。また、せん断面の角度によって、作用する垂直応力やせん断応力の働き方が変化します。

ここで重要なのは働いている応力という存在は変わっていないのに、見方を変えれば値が変わることです。ベクトルでも、同じベクトルという存在が変わらなくても基底ベクトルを変えれば異なった数式になりますね。

\[\vec{b} = b_1 \vec{e_1} + b_2 \vec{e_2} + b_3\vec{e_3} = b_i\vec{e_i}\]

\[\vec{b} = \bar{b_1} \bar{\vec{e_1}} + \bar{b_2} \bar{\vec{e_2}} + \bar{b_3}\bar{\vec{e_3}} = \bar{b_i}\bar{\vec{e_i}}\]

式で書けばこのようになります。応力の場合は、力というベクトルだけでなく、どの面を切り取って見るか？という情報を持っているのでベクトルより情報が多いわけです。このような場合にテンソルを利用します。ちなみに応力は２階のテンソルです。

また応力テンソルの場合、下の図のように、どのような面に働く力を考えるか？という情報を決めると、その面に働く応力のベクトル\(\vec{t_n}\)を観測することができる。ここで注目する断面の法線ベクトル\(\vec{n}\)とすると、応力テンソルを\(\vec{T}\)と書くなら、

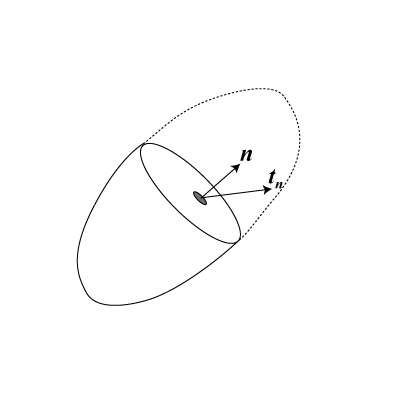
\[\vec{t_n} = \vec{T}(\vec{n})\]

と表される。このようにテンソル\(\vec{T}\)はベクトル\(\vec{n}\)から\(\vec{t_n}\)への変換を表すものとも見ることができますね。以後の定義は、２階のテンソルについて説明します。

テンソルの定義

上の説明のように、テンソルは任意のベクトル\(\vec{n}\)に対し、\(\vec{t_n}\)を生じさせる変換で、テンソル\(\vec{X}\)の定義は、任意のベクトル\(\vec{a},\vec{b}\)を使って

\[\vec{a}\otimes\vec{b}=\vec{X}\]

と表現できます。ここで\(\vec{a}\otimes\vec{b}\)はテンソル積とよばれ、ディアドやダイアドと呼ばれます。このテンソル積は、ベクトル\(\vec{c}\)を次のように変換する式として定義されます。

\[(\vec{a}\otimes\vec{b})\cdot \vec{c} =(\vec{b}\cdot\vec{c})\vec{a}\]

この式は、とても重要なので覚えておきましょう。式を入れ替えれば明らかにわかりますが、

\[\vec{a}\otimes\vec{b}\neq\vec{b}\otimes\vec{a}\]

となります。次に、実数\(a_1, a_2, a_3, \cdots , a_n\)を使ったテンソル積の１次結合

\[a_1(\vec{a_1}\otimes\vec{b_1})+a_n(\vec{a_n}\otimes\vec{b_n})+\cdots+a_n(\vec{a_n}\otimes\vec{b_n})\]

もテンソルとなります。これをディアディックと呼びます。キルア=ゾルディックとは無関係です。

また、基底ベクトルと、9個の係数\(X_{ij} i=1,2,3, j=1,2,3\)から、次のようにディアディック表示が可能です。この式もたびたび出てきます。

\[\vec{X}=X_{ij} \vec{e_i} \otimes\vec{e_j}\]

この記事はここまで。基本的な定義式なので、何度も出てきます。もし忘れたら、またこのサイトに戻ってきたり、ノートを見たりして復習してください。